批量计算线路标高

本文由简悦 SimpRead 转码，原文地址 zhuanlan.zhihu.com

我的使用场景可以简化为：给定一段纵段面数据，把他放到 Excel 中。打开一个写有里程的 Excel 表，点击运行程序，在每个里程单元格后边显示对应的标高。

轨面标高计算原理

直线段的标高

直线段的坡度计算非常好计算。线路纵断面图中已给出了线路纵断面在变坡拐角时的标高，我们只需要按坡度乘以里程间隔再加下变坡点的标高就可以了。
H=H_1+L\times i \tag{1}

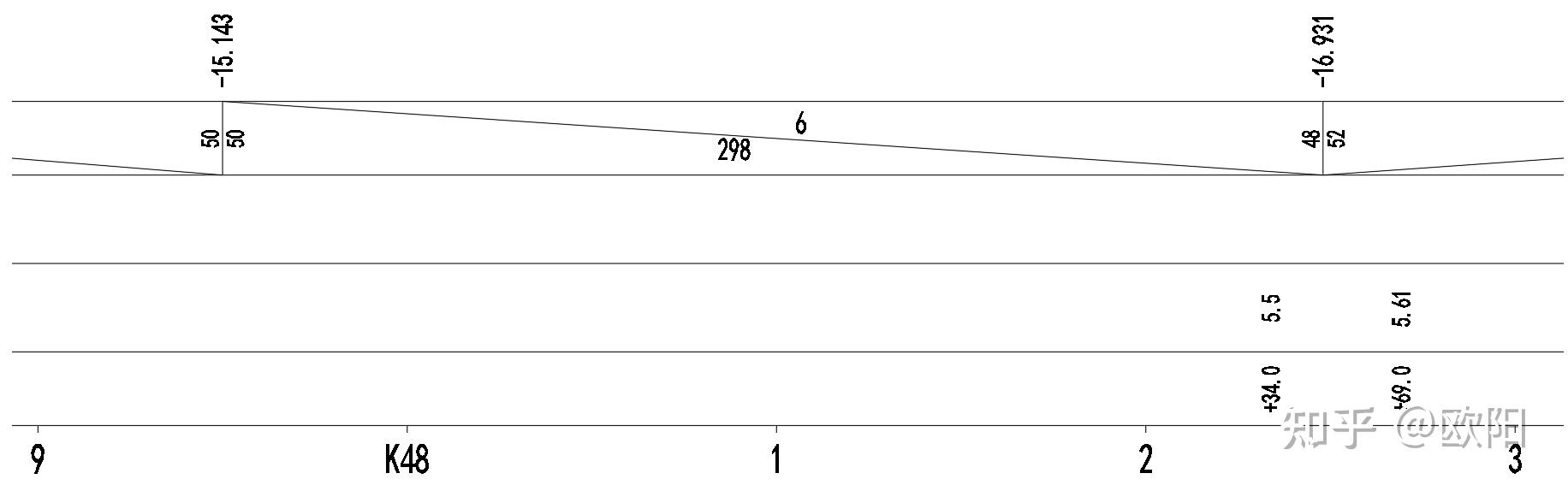
不过由于显示精度的问题，个别情况下同一里程，从左向右计算的标高与从右向左计算的标高，在毫米精度上有时会稍有不同，一般问题不大。

竖曲线段的标高

由于钢轨在线路拐角时不是按折角的，要有一个竖曲线衔接。典型的竖曲线要素就是变坡点里程，竖曲线的半径及切线长。竖曲线位置的标高计算相对比较麻烦些。一般而言主要计算思路就是按直线段的坡度的计算出来的标高考虑加上或减去由于竖曲线带来的偏差修正值（这个偏差即外矩δ）即：
H=H_1+L\times i+\delta \tag{2}
后边我们会涉及另外一种计算方法，在编程时比这个更好用。

我们先假设一个圆形竖曲线，两侧分别接坡度为i_1 和i_2的直线，连接两个斜线的曲线公式为：
y=ax^2+bx+c\tag{3}
x 轴是我们的线路里程，y 轴是我们的轨面标高, 曲线的切线长为 T。曲线前后衔接的两个直线为：
y_1=i_1x+c_1\tag{4}
y_2=i_2x+c_2\tag{5}
在文章线路最低点计算中我们已经计算了曲线公式中的参数。其中:\begin{aligned}a = \frac{i_2-i_1}{4T}\\b=i_1\\ c=-Ti_1\end{aligned}\tag{6}
由于竖曲线的起点坐标是即(0,-Ti_1)，第一条直线亦过此点则可得:
c_1=c=-Ti_1\tag{7}
又由于第二条直线与 x 轴的交点为(T,0)则:
c_2=-Ti_2\tag{8}
我们先计算下同一里程处，第一个直线与竖曲线间的修正值大小：
\delta=y-y_1=\frac{i_2-i_1}{4T}x^2\tag{9}
我们在线路最低点计算中已经证明过下述公式：
R=\frac{1}{|y''|}=|\frac{2T}{i_1-i_2}|=\frac{2T}{-i_1+i_2}\tag{10}
故:
\delta=\frac{x^2}{2R}
当 x=T 时，可以得到曲线的外矢矩为e=\frac{T^2}{2R}，这个参数在本文中没有什么用，我一般用于计算验证。由于我们设置的坐标系里程 O 点位于曲线切线起点位置，故上式中的 x 值应该是第一条线曲线的起点开始计，这一点很重要。

对于第二条曲线情况应该是一样的，可以直接仿照第一第线的结果直接套第二条线，但这并不妨碍我们再次通过对第二条直线的修正值的计算来进行证明这个结论：
\begin{align} \delta &= y - y_2 \\ &= \frac{i_2 - i_1}{4T} x^2 + i_1 x - Ti_1 - (i_2 x - i_2 T) \\ &= \frac{x^2}{2R} + x(i_1 - i_2) + T(i_2 - i_1) \\ &= \frac{x^2}{2R} - \frac{2T}{R} x + \frac{2T^2}{R} \\ &= \frac{x^2 - 4Tx + 4T^2}{2R} \\ &= \frac{(x - 2T)^2}{2R} \end{align}\\ \tag{12}
由于竖曲线的终点里程为 2T，故按第二个曲线计算修正值时亦是按计算位置与曲线终点的里程差除以 2R 得到。

综上，这样就得到了线路纵断面的计算原理。

Python 程序编制

总体思路

在 vscode 中打开程序，运行。打开要计算的里程表，先择线路纵断面数据。程序选择一个里程判断是否在竖曲线上，如果在竖曲线上执行竖曲线标高计算程序，如果在直线段则执行直线段的标高计算程序。把结果写入表格。再选择下一个里程进行上述计算，直至计算完毕。

实现过程

竖曲线地段标高计算函数

首先我们来实现第一个基本函数——竖曲线地段的标高计算。这个函数有两种实现方法：

第一种就是我们按本章公式（2）的方式，就是通过先计算线性坡度的标高再通过修正值进行修正。这种方法更适合手算，因为其中有很多工况、前提条件等等，我们通过脑袋已经自动处理了，同时计算公式也更容易记忆。
第二种方法是我们直接引用竖曲线的公式，即公式（6）计算出标高后再通过变坡点的标高来修正。第二种方法更适合编程，虽然参数相对复杂但对于编程来说不是问题。

虽然第二种方法更简单。但是为了展示两种方法的不同，我们两种方法都试下。

方法一、按直线坡度计算后再修正

观察公式（2），当所计算的里程小于变坡点里程时，坡度值需要用 i_1，当计算里程大于变坡点里程时，坡度就需要用 i_2, 因此就需要分情况讨论。但此时还没有完。每一种情况下还得再分两种情况：

第一种：当i_2-i_1>0时，如下图两种情况所示。此时图形是上凹的，即竖曲线在切线的上方。

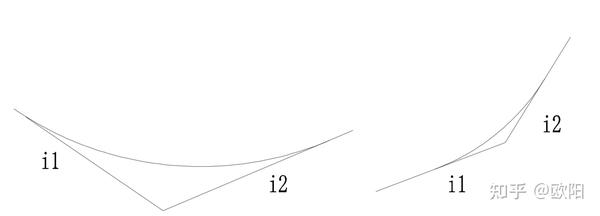
第二种：i_2-i_1时，如下图所示，此时图形时下凹的。即竖曲线在切线的下方。

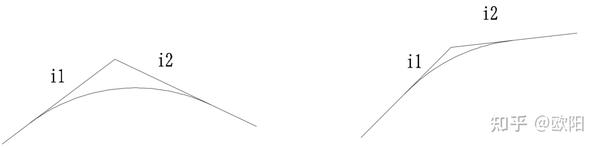
于是我们在函数中也需要按四种情况进行计算：代码如下：

def bian(x,y):  #参数x是要计算的里程，y是我们的基础参数
    t=x[0];b=x[1];r=x[2] #t是切线长，b是变坡点里程，r是竖曲线径  
    i1=x[3];i2=x[4];gao=x[5] #i1是前坡长，i2是后坡长，gao是变坡点线路标高
    i1=i1/1000   #将坡度转换为
    i2=i2/1000
    s=b-t          #计算竖曲线起始里程
    e=b+t          #计算竖曲线终点里程
    if s<=y and y<=e:   
        pass
    else:
        print('检查输入的里程')
        raise Exception("里程超出.")
    if y<b:    #第一种情况：计算里程小于变坡点里程
        if (i2-i1>0):  #曲线是上凹的
            aq=gao-i1*(b-y)+(y-s)**2/2/r
        else:           #曲线是下凹的
            aq=gao-i1*(b-y)-(y-s)**2/2/r
    else:    #第二种情况：计算里程大于变坡点里程
        if (i2-i1>0): #曲线是上凹的
            aq=gao+i2*(y-b)+(e-y)**2/2/r
        else:          #曲线是下凹的
            aq=gao+i2*(y-b)-(e-y)**2/2/r
    aq=round(aq,3)
    return aq

可以看出第一种情况是比较麻烦的。但是这种方法在手算时相当友好。我最初编程时就是因为习惯而采用了该种方法，在写这篇文章的时候，我改为了第二种方法。

方法二、采用竖曲线公式再修正

这种法相对而言要简单的多。我们只需要把公式（6）代入竖曲线中，再加上变坡点的标高就可以了。

def bian(x,y): #与方法一样的函数
    t=x[0];b=x[1];i1=x[2];i2=x[3];gao=x[4]
    i1=i1/1000   #将坡度转换
    i2=i2/1000
    s=b-t          #计算起始里程
    e=b+t          #计算终点里程
    if s<=y and y<=e:
        pass
    else:
        print('检查输入的里程')
        raise Exception("里程超出.")#这之前都与方法一是一样。
    aa=(i2-i1)/4/t
    bb=i1
    cc=-t*i1
    aq=gao+aa*(y-s)**2+bb*(y-s)+cc
    return aq

另外我们也可以看出方法二中需要输入的参数是没有 R 的。因为 R 是可以计算来的，所以也就没有必要再输入了。后续我们直接采用第二方法计算。

考虑断链的线路长度计算函数

第二个比较重要的函数就是考虑断链的两个里程间的长度。这个函数主要应用于计算直线段标高时，计算里程与起始里程间的真实长度。和线路专业沟通后，断链一般不会设置在竖曲线上。目前为止我也的确没有遇到过。故这种情况不再讨论。

def changdu(qujian,biao):  #输入的是一个里程区间qujian和一个断链表biao
    length=len(biao) #断链表的长度

    zong=qujian.sup-qujian.inf # 区间的上限减去下限，得到区间的名义长度

    for i in range(0,length-1): #对断链表中的每一行进行判断，看他是否在计算区间中。若在，那应该把断链值加到区间长度中。

        if biao[i,0] in qujian:

            zong=zong+biao[i,2]        

    return zong

但是需要说明的一点是由于线路里程中存在断链，短链一般不影响，但是对于长链，说明一个线路中存在一段里程同时出现了两次，程序不能仅靠里程值判断，这个值是第一个里程还是第二个里程。默认为第一个里程。

直线段的线路标高函数

直线段的轨面标高计算很简单，按公式（1）即可。

def zhi(qig,i,chang): #输入起点标高qig,坡度i,距离chang

    gao=qig+i/1000*chang

    return gao

总标高计算函数

接下来我们把上边三个函数汇总到一起，定义一个总的计算标高的函数。总体思路是，给定一个里程，查看他是否在竖线线范围，如果是，则执行竖曲线标高计算函数，如果不是，核实里程在哪个直线段，再执行直线段的标高计算公式。

#每一个竖曲线的起终点生成一个区间，再把前后竖曲线的变坡点里程生成区间。

def biaogao(licheng,npd,ndl):  #设置一个函数，需要输入里程值和数据源numpy array

    chang=len(npd) #坡度表的行数

    # 计算竖线曲线标高

    for i in range(0,chang):

        gao=npd[i,0];b=npd[i,1];t=npd[i,2];i1=npd[i,3];i2=npd[i,4]

        st=b-t  #竖曲线的起点里程

        ed=b+t  #竖曲线的终点里程

        a=Interval(st,ed)  #每一个竖曲线的起终点生成一个区间

        if licheng in a:  #如果要判断的里程在这个竖曲线的曲间

            x=[gao,b,t,i1,i2]

            return bian(x,licheng)

    #计算直线标高

    for j in range(0,chang-1):

        t1=npd[j,2] #第一个竖曲线的切线长

        t2=npd[j+1,2] #第二个竖曲线的切线长

        b1=npd[j,1] #第一个竖曲线的变坡点

        b2=npd[j+1,1] #第二个竖曲线的变坡点

        st=b1+t1  #第一个竖曲线的终点

        ed=b2-t2  #第二个竖线的起点

        a=Interval(st,ed)  #两个竖曲线之间的直线生成一个区间

        if licheng in a:   #判断里程是否在直线上

            jisuan=Interval(b1,licheng) #在第一个变坡点里程和计算里程之间形成一个计算区间。

            ch=changdu(jisuan,ndl)     #计算里程与第一个竖曲线变坡点的实际长度。

            jieguo=zhi(npd[j,0],npd[j,4],ch) #直线段的标高计算

            return jieguo

Excel 计算

首先我们把需要计算的基础数据输入表格中。我们以某城市地铁一个区间的线路纵断面作为输入，如下：

断链表，我们也需要输入：

另外我们把需要把计算的里程放到一个新的 EXCEL 中，不放也可以，为了程序执行的标准化，我们把还是放到一个新的 EXCEL 中比较好。

接下来我们就可以计算了。

app=xw.apps.active #获取当前活动的excel进程

wb = app.books.active #获取当前活动的表格

datasht=wb.sheets[0] #获取第一个sheet，也就是需要计算的里程表。

shu=len(datasht.range('A1').expand(mode='down')) #需要求解的里程数量

for i in range(0,shu):

    datasht[i+1,1].value=biaogao(datasht[i+1,0].value,npd)

结果展示

计算结果与铺轨单位的计算工具在毫米级是一样的，说明该程序是有效、可用、便捷的。

代码汇总

from sympy import Interval
import os
import numpy as np  
import pandas as pd
import xlwings as xw
import tkinter as tk
from tkinter import filedialog

#-------------------------------------------------

lujing=os.getcwd()

rt=tk.Tk()

rt.withdraw()

file_path=filedialog.askopenfilename(title="请选择输入资料：",

                                    initialdir=lujing,

                                    filetypes = (("xlsx files","*.xlsx"),))

nlj=os.path.dirname(file_path)
os.chdir(nlj)
pdb=pd.read_excel(file_path,'坡度表') #得到坡度表
dlb=pd.read_excel(file_path,'断链表') #得到断链表

#为了方便操作将DataFrame转换为numpy

npd=np.array(pdb)
ndl=np.array(dlb)

#-------------------------------------------------------------

#定义了一个函数用于计算每个变坡点附近曲线范围内的线路标高
#s即起始里程start；e为终点里程end；b为边坡点里程;t是切线长；r为半径radius;
#i1即前坡度,i2即后坡度,gao为边坡点的高程。

def bian(x,y): #竖曲线标高计算函数
    gao=x[0];b=x[1];t=x[2];i1=x[3];i2=x[4]
    i1=i1/1000  #将坡度转换
    i2=i2/1000
    s=b-t #计算起始里程
    e=b+t #计算终点里程
    if s<=y and y<=e:
        pass
    else:
        print('检查输入的里程')
        raise Exception("里程超出.")
    aa=(i2-i1)/4/t
    bb=i1
    cc=-t*i1
    aq=gao+aa*(y-s)**2+bb*(y-s)+cc
    return aq
#---------------------------------------------------------
#定义一个方函数用来计算两个里程之间考虑断链后的实际长度。
def changdu(qujian,biao):  #输入的是一个里程区间qujian和一个断链表biao（array）
    length=len(biao)
    zong=qujian.sup-qujian.inf
    for i in range(0,length-1):
        if biao[i,0] in qujian:
            zong=zong+biao[i,2]        
    return zong
#-------------------------------------------------------

#直线段的标高计算函数
def zhi(qig,i,chang): #输入起点标高qig,坡度i,距离chang
    gao=qig+i/1000*chang
    return gao
#------------------------------------------------------  
#每一个竖曲线的起终点生成一个区间，再把前后竖曲线的变坡点里程生成区间。
def biaogao(licheng,npd,ndl):  #设置一个函数，需要输入里程值和数据源numpy array
    chang=len(npd) #坡度表的行数
    # 计算竖线曲线标高
    for i in range(0,chang):
        gao=npd[i,0];b=npd[i,1];t=npd[i,2];i1=npd[i,3];i2=npd[i,4]
        st=b-t  #竖曲线的起点里程
        ed=b+t  #竖曲线的终点里程
        a=Interval(st,ed)  #每一个竖曲线的起终点生成一个区间
        if licheng in a:  #如果要判断的里程在这个竖曲线的曲间
            x=[gao,b,t,i1,i2]
            return bian(x,licheng)
    #计算直线标高
    for j in range(0,chang-1):
        t1=npd[j,2] #第一个竖曲线的切线长
        t2=npd[j+1,2] #第二个竖曲线的切线长
        b1=npd[j,1] #第一个竖曲线的变坡点
        b2=npd[j+1,1] #第二个竖曲线的变坡点
        st=b1+t1  #第一个竖曲线的终点
        ed=b2-t2  #第二个竖线的起点
        a=Interval(st,ed)  #两个竖曲线之间的直线生成一个区间
        if licheng in a:   #判断里程是否在直线上
            jisuan=Interval(b1,licheng) #在第一个变坡点里程和计算里程之间形成一个计算区间。
            ch=changdu(jisuan,ndl)            #计算里程与第一个竖曲线变坡点的实际长度。
            jieguo=zhi(npd[j,0],npd[j,4],ch) #直线段的标高计算
            return jieguo
#-------------------------
#以下是我们提取一个打开的EXCEL表格，按每个里程进行标高计算
app=xw.apps.active
wb = app.books.active
datasht=wb.sheets[0] #获取第一个sheet
shu=len(datasht.range('A1').expand(mode='down'))-1 #需要求解的里程数一共有x个。

for i in range(0,shu):
    datasht[i+1,1].value=biaogao(datasht[i+1,0].value,npd,ndl)

本文使用 Zhihu On VSCode 创作并发布